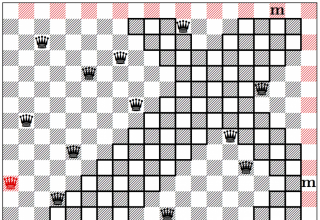
هر ساله مسابقات مختلفی در حوزههای برنامهنویسی، امنیت و بازیهای کامپیوتری در سراسر جهان برگزار میشود. در این مسابقات مردم سراسر جهان تلاش میکنند در کوتاهترین زمان ممکن بهترین و در عین حال سادهترین راهکار برای حل مسائل را ارائه کنند. اما گروهی از پژوهشگران دانشگاه سنت اندروز مسئله معروف معمای وزیر (مهرههای وزیر در صفحه شطرنج) را پیشنهاد کردهاند. در مسئله سنتی که اولین بار در سال 1848 مطرح شد باید 8 وزیر را روی صفحه استاندارد 64 خانهای به گونهای قرار میدادید که قادر نباشند یکدیگر را حذف کنند. به عبارت دقیقتر هیچکدام از مهرهها نباید در یک ستون و ردیفی قرار میگرفتند که که یکدیگر را هدف قرار دهند. زیبایی چالش فوق این است که شما واقعا نیازی ندارید قوانین بازی شطرنج را بلد باشید. اما این به معنای آن نیست که چالش فوق ساده خواهد بود. مشکل سنتی را حداقل به 92 شکل مختلف میتوان حل کرد. اما زمانی که ابعاد صفحه از 8 در 8 بیشتر شود چه میکنید؟ اگر تعداد وزیرها به 20 وزیر یا 100 در 100 وزیر برسد چه خواهید کرد؟ حال اگر تعداد وزیرها به 1000 عدد برسد چه خواهید کرد؟ بدون شک محاسبه تعداد ردیفها، سطرها و ستونها در حالت واقعی کار بسیار پیچیدهای خواهد بود.

حل مشکل 8 وزیر در دنیای واقعی کار سادهای به شمار میرود. اما مشکل زمانی آغاز میشود که در نظر داشته باشید به کامپیوتر اعلام کنید چنین کاری را انجام دهد. زمانی که تصمیم میگیرد صفحه شطرنج و عملکرد مهرههای مختلف شطرنج را در قالب برنامهای برای یک کامپیوتر تعریف کنید در عمل باید پردازشهای بسیار زیادی برای بررسی شرایط مختلف بازی انجام شود. در نتیجه کامپیوتر به زمان و انرژی زیادی نیاز دارد. همچنین اگر برنامهنویسی شما به درستی انجام نگرفته باشد خیلی زود با پیغام سرریز بافر روبرو میشوید. مقالهای که به تازگی در مجله هوش مصنوعی به چاپ رسیده اعلام میدارد اگر صفحه شطرنج ابعادی 1000 در 1000 داشته باشد حل این مسئله کاملا ساده برای کامپیوترها به چالشی غیر ممکن تبدیل میشود. در نتیجه اگر الگوریتمی برای حل مشکل n-Queens ارائه شود تا بتواند ساختار فوق را با سرعت بالایی پیادهسازی کند به احتمال زیاد از همین تکنیک برای حل مسائل رام نشدنی هوش مصنوعی نیز میتوان استفاده کرد. معمای هشت وزیر شبیه به مسئله دیگری در حوزه علوم کامپیوتری است که به مسئله P در برابر NP شهرت پیدا کرده است. این مسئله میگوید آیا مشکلی که به شکل سریعی قابل حل شدن است را میتوان از طریق راهکار سریعتری نیز حل کرد؟
در نهایت اگر موفق شوید برای مسئله وزیر در ابعاد 1000 در 1000 راهحل سریعی ابداع کنید و رقیبی نداشته باشید موفق خواهید شد جایزه یک میلیون دلاری را از آن خود کنید.