مسائل به ظاهر ساده اما حل نشده دنیای ریاضیات
همهی ما میدانیم که ریاضیات بسیار سخت است؛ آنقدر سخت که یک صفحه از ویکیپدیا به مسائل حلنشده ریاضی اختصاص دارد. این درحالی است که بسیاری از باهوشترین افراد دنیا همیشه درحال کار کردن روی این مسائل بودهاند.
اما همانطور که اوری تامپسون در پاپیولار مکانیک اشاره میکند، این مسائل حداقل در ابتدای راه بسیار ساده به نظر میرسند؛ آنقدر ساده که هرکسی با دانشی ابتدایی از ریاضی میتواند آنها را درک کند؛ اما متأسفانه اثبات این مسائل بسیار سخت است. ما از لیست تامپسون استفاده کردیم و فهرست خودمان را از مسائل بهظاهر ساده ریاضی که البته حلشان مشکل است ارائه دادیم؛ به این امید که شاید شما را به خود جذب کند.
حدس اعداد اول دوگانه
اعداد اول، اعدادی هستند که تنها بر خودشان و ۱ بخشپذیر هستند. تا آنجاییکه ما میدانیم، تعداد اعداد اول بیشمار است و ریاضیدانان سخت درتلاش برای یافتن بزرگترین عدد اول بعدی هستند.
اما تعدادی از اعداد اول هستند که حاصل تفریق آنها ۲ است، مثل ۴۱ و ۴۳. آیا تعداد این اعداد نیز بینهایت است؟ هرچه اعداد اول بزرگتر میشوند، یافتن این دوقلوها سختتر میشود؛ اما از لحاظ تئوری این اعداد نیز باید بینهایت باشند. مشکل اینجا است که هنوز هیچکسی نتوانسته این بینهایت بودن اعداد اول دوگانه را اثبات کند.
مسئله حرکت دادن مبل
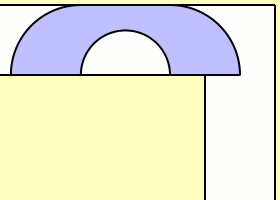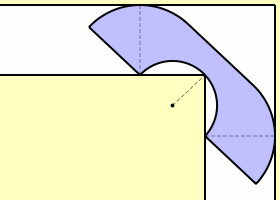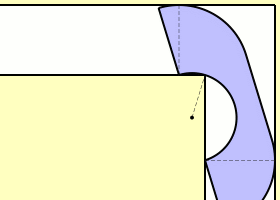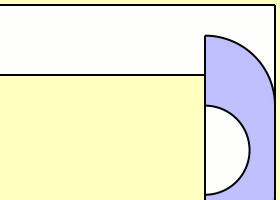
این مشکلی است که اکثر ما احتمالا با آن دست و پنجه نرم کردهایم و زمان اثاثکشی به یک آپارتمان جدید و آوردن مبل به آن ساختمان، با آن برخورد کردهایم. البته شما باید برای آوردن مبل به اتاق نشیمن آن را از گوشهای عبور دهید. ریاضیدانان میخواهند بدانند بزرگترین مبلی (بدون در نظر گرفتن شکل) که میتوانید بدون خم کردن آن، از زاویهی ۹۰ درجه عبور دهید چقدر است (ریاضیدانان به این مسئله از جنبه دوبعدی نگاه میکنند). تامپسون توضیح میدهد:
بزرگترین منطقهای که با گوشه و زاویه سازگار درمیآید، ثابت مبل نامیده میشود. هیچکس بهطور دقیق نمیداند این عدد چقدر است؛ ولی ما مبلهای بزرگی داریم که میدانیم این عدد حداقل بهبزرگی آنها است. ما همچنین مبلهایی داریم که اندازهی آنها با این مقدار سازگار نیست، پس این اندازه از آنها کوچکتر است. درمجموع میدانیم که ثابت مبل چیزی بین ۲.۲۱۹۵ تا ۲.۸۲۸۴ است.
حدس کولاتز
حدس کولاتز یکی از مشهورترین مسائل حلنشدهی ریاضی است و از آنجایی که بسیار ساده به نظر میرسد، میتوانید آن را برای بچههای مدارس ابتدایی توضیح دهید و آنها احتمالا آنقدر به این مسئله جذب خواهند شد که سعی کنند جوابی برای آن پیدا کنند. مسئله اینگونه است: ابتدا یک عدد انتخاب میکنید (فرقی ندارد چه عددی).
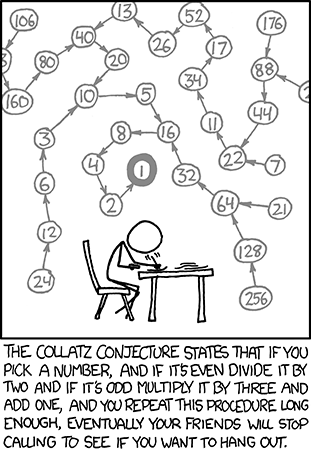
اگر این عدد زوج بود، آن را به ۲ تقسیم کنید و اگر فرد بود آن را در ۳ ضرب و سپس با ۱ جمع کنید. این پروسه را برای عدد جدید بهدستآمده ادامه دهید. عددی که سرانجام به آن میرسید همیشه ۱ خواهد بود (بهعنوان مثال اگر عدد انتخابی ۶ باشد: ۶، ۳، ۱۰، ۵، ۱۶، ۸، ۴، ۲، ۱).
این قاعده بسیار ساده به نظر میرسد و واقعا جواب میدهد. ریاضیدانان میلیونها عدد را پیدا کردهاند که تابع این قاعده است؛ اما مشکل اینجا است نتوانستهاند عددی پیدا کنند که طبق این قاعده پیش نرود. تامپسون توضیح میدهد:
احتمال دارد که عددی بسیار بزرگ که میل به بینهایت دارد یا عددی که در یک چرخه گیر کند، هرگز به ۱ نرسد؛ ولی تابهحال کسی نتوانسته است این عدد را پیدا کند و آن را ثابت کند.
حدس بیل
حدس بیل اینگونه است:
اگر Ax + By = Cz و A ،B ،C،اx،اy و z همگی اعداد صحیح مثبت باشند ( اعداد بزرگتر از ۰)، A ،B و C باید همگی یک عامل اول مشترک داشته باشند. عامل اول مشترک بدین معنا است که هر یک از این اعداد باید بر عدد اول یکسانی پخشپذیر باشد. مثلا عامل اول مشترک اعداد ۱۵، ۱۰ و ۵ برابر است با ۵ (همه آنها بر عدد اول ۵ بخشپذیرند.)
این مسئله تا اینجا ساده به نظر میرسد و شاید نمونه آن را در درس جبر دبیرستان حل کرده باشید. اما مشکل اینجا است که ریاضیدانان هنوز نتوانستهاند حدس بیل را با x، y و z بزرگتر از ۲ حل کنند. بهعنوان مثال اگر عامل اول مشترک ما ۵ باشد:
۵۱ + ۱۰۱ = ۱۵۱
اما
۵۲ + ۱۰۲ ≠ ۱۵۲
جایزهای ۱ میلیون دلاری برای کسی که بتواند بهطور کارشناسی این مسئله را ثابت کند، در نظر گرفته شده است؛ پس شروع به اثبات آن کنید.
مسئله مربع محاطی
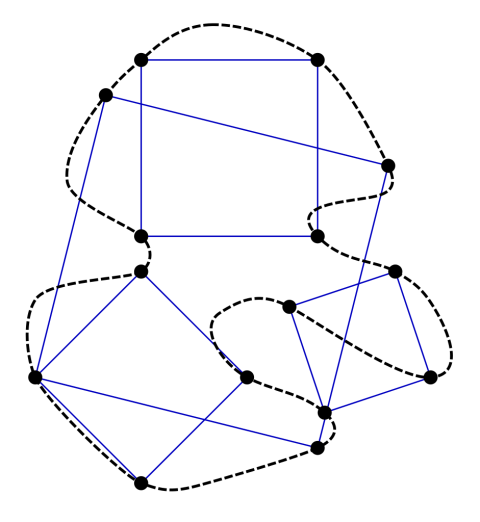
این مسئله نیازمند کمی رسم شکل است. روی یک کاغذ، یک شکل حلقهمانند بکشید ( لزوما نباید شکل خاصی باشد و تنها باید یک حلقه بسته که خودش را قطع نکند کافی است). بر اساس فرضیهی مربع محاطی داخل این حلقه، شما باید بتوانید مربعی بکشید که تمام چهار گوشهی آن روی خط تشکیلدهندهی حلقه باشد. این کار به نظر ساده میرسد؛ اما از نظر ریاضی، تعداد احتمالات شکلهای حلقه بسیار زیاد است و ممکن نیست بگوییم آیا میتوان مربعی رسم کرد که تمام گوشههای آن روی حلقه قرار بگیرد. تامپسون مینویسد:
این مسئله برای تعدادی دیگر از اشکال هندسی مثل مثلث و مستطیل حل شده است؛ اما اینکه برای مربع هم جواب خواهد داد یا خیر، کمی مبهم است و تاکنون اثباتی از سوی ریاضیدانان صورت نگرفته است.
حدس گلدباخ
این مورد که شبیه به حدس اعداد اول دوگانه است، مسئلهی ساده دیگری در حوزهی اعداد اول است و به دلیل پیچیدگی درعین سادگی، شهرت دارد. مسئله اینجا است که آیا میتوان هر عدد صحیح زوج بزرگتر از ۲ را بهصورت مجموع دو عدد اول نوشت؟ ابتدا اینگونه به نظر میرسد که پاسخ مثبت است؛ مثلا عدد ۴ مجموع دو عدد اول ۳ و ۱ یا عدد ۶ مجموع دو عدد اول ۵ و ۱ است و این روند ادامه دارد.
اما با وجود سالها تلاش، تابهحال هیچکس نتوانسته است ثابت کند که این قاعده همیشه و برای همه اعداد جواب میدهد. حقیقت این است که اگر ما اعداد را بزرگ و بزرگتر کنیم و بههمین روند ادامه دهیم، شاید به عددی برسیم که برابربا مجموع دو عدد اول نباشد یا عددی که تمامی قوانین و منطقی که تابهحال از آن استفاده میکردیم نقض کند. مطمئن باشید ریاضیدانان تا جوابی برای این مسئله پیدا نکنند از کار خود دست نخواهند کشید.
برگرفته از SCIENCEALERT